취준 때문에 바빠서 2주만에 돌아왔다.
다시 꾸준히 글을 쓰려고 한다.
[알고리즘 포스팅 순서]
1. 시간복잡도
2. 배열
3. 연결리스트
4. 스택
5. 큐
6. 트리
7. 그래프
8. 해쉬테이블
9. 정렬(선택, 버블, 삽입, 퀵, 힙, 병합)
10. 코테 대비 백준 문제 풀이 꿀팁
[서론]
난 많은 자료구조 중에서 이 '트리' 개념 때문에 초반에 자료구조의 전체적인 흐름을 이해하기가 힘들었다.
용어도 많고 종류도 많고 관련 글도 많아서 복잡해서였다.
그래서 이 답답함을 해소하기 위해 이 알고리즘 시리즈를 시작한 것이라고 해도 과언이 아니다.
'트리'에 대한 모든 것을 초! 간단하게 낱낱히 파헤치고자 한다.
[트리란?]
트리(Tree)란 노드들이 나뭇가지처럼 연결되어 있는 비선형 자료구조를 의미한다.
트리는 다음에 나올 그래프(Graph)의 일종인데 순환(cycle)이 없는 연결 그래프라고도 한다.
다음과 같이 나무를 거꾸로 매단 것처럼 보이는 모양과 유사하다.

트리 안에 트리가 존재하는 재귀적인 특징을 가지고 있으며
일상 예시로는 컴퓨터의 디렉토리 파일 저장 방식, 회사의 조직도, 집안의 족보 모양과 비슷하다.
[구조와 기능]

1. 용어 (많다고 겁먹지 말자 차근차근 이해하면 쉽다!)
- 노드(node): 데이터(값)과 포인터(다음 노드와의 연결점)를 가지고 있는 트리의 필수 요소
- 간선(edge): 노드와 노드 사이를 잇는 연결선
- 루트(root) 노드: 부모 노드가 없는 최상위 노드. 모든 트리의 루트는 하나다.
- 부모(parent) 노드: 자식(child) 노드를 가진 노드
- 자식(child) 노드: 부모(parent) 노드의 하위 노드
- 형제(siblings) 노드: 부모(parent)가 같은 노드
- 리프(leaf) 노드: 자식(child)이 없는 노드 (외부 노드, 단말 노드라고도 함 <-> 가지노드, 내부노드, 비단말노드)
- 서브 트리(sub tree): 특정 노드를 루트로 생각할 때 생기는 트리
기타 용어
- 크기(size): 자신을 포함한 모든 자식 노드의 개수
- 레벨(level): 루트 노드부터 특정 노드까지 연결된 간선의 수
- 깊이(depth): 루트 노드부터 특정 노드까지의 거리, 수치로만 보면 레벨과 같은 것 같다.
- 높이(height): 특정 노드에서 가장 깊은 노드까지의 길이
- 경로(path): 한 노드에서 다른 노드로 갈 때 거쳐 가는 노드들의 순서
- 거리(distance): 두 노드 사이의 최단 경로에 있는 간선의 수
- 차수(degree): 자식 노드의 개수
- 넓이(breadth): 리프 노드의 갯수
2. 특징
- 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있다.
- 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조이다.
- 트리내에 또 다른 트리가 있는 재귀적 자료구조이다.
- 단순 순환(Loop/cycle)을 갖지 않고, 연결된 무방향 그래프이다.
- 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖는다.
- 노드가 n개인 트리는 항상 n-1개의 간선(edge)을 갖는다.
다음은 트리가 아닌 것의 예시다
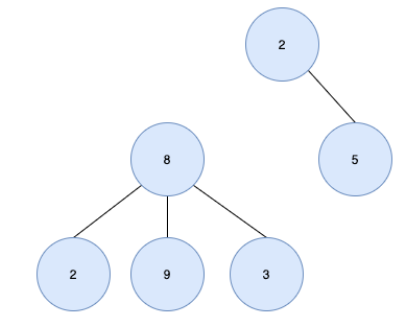
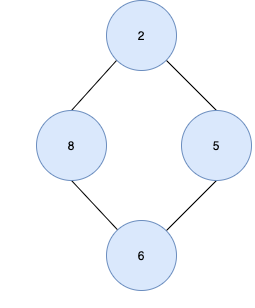
3. 트리의 종류
- 이진트리 (binary tree): 각 노드의 차수(자식 노드)가 2개 이하인 트리
(이진 트리를 많이 사용함) - 삼진트리 (ternary tree): 각 노드의 차수(자식 노드)가 3개 이하인 트리
- 이진탐색트리 (binary serch tree): 순서가 있는 이진 트리,
왼쪽 자식 노드는 부모 노드보다 작은 값을 가져야하며 오른쪽 자식 노드는 부모 노드보다 큰 값을 가져야 한다.
(이 '탐색'이라는 용어는 균형탐색트리 등등으로 발전할 수 있다. 이진탐색트리 관련해서는 참고문헌5. 참고하시길)

- 균형트리 (balanced tree, B-tree): 좌우 서브 트리 높이가 1보다 크게 차이나지 않는 트리
- 편향트리 (skewed tree): 좌우 서브 트리 높이가 1보다 크게 차이나서 한쪽으로만 편향된 트리

- 완전이진트리 (complete binary tree): 마지막 노드를 제외하고 모든 노드의 자식이 0이며 마지막 레벨의 노드는 왼쪽에 채워져 있는 트리

- 포화이진트리 (full binary tree): 모든 노드의 자식이 0이거나 2인 이진 트리

- 완벽이진트리(perfect binary tree): 루트 노드부터 리프 노드까지 빈 공간 없이 채워진 트리

4. 사용 사례
- 계층적 데이터 저장
- 효율적인 검색 속도
- 힙(Heap): 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
빠른 최댓값, 최솟값 찾기에 유용하다. (힙도 중요한 개념인데 참고문헌6. 을 참고하길 바란다.) - 데이터 베이스 인덱싱
- 예) B-Tree, B+Tree, AVL-Tree(참고문헌7), Red-Black-Tree(참고문헌8) 등
- Trie트리: 사전을 저장하는 데에 유용한 트리
[코드]
이번 트리 코드는 추후에 추가하도록 하겠다.
트리는 용어도 많고 종류도 많고 사용 사례도 많다.
코테나 코딩대회에서도 이진탐색 관련된 문제는 많이 나오므로 트리 개념 숙지는 필수다!
(사실 모든 자료구조 기본 개념은 중요하지만 B-Tree같은 세부적인건 넘겨도 된다)
[참고문헌]
1. 위키백과: https://wikidocs.net/193702
2. 블로그: https://yoongrammer.tistory.com/68
3. 블로그: https://wonit.tistory.com/198
4. 동영상: https://www.youtube.com/watch?v=LnxEBW29DOw&list=PLjSkJdbr_gFY8VgactUs6_Jc9Ke8cPzZP
5. 블로그(binary seach tree): https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
6. 블로그(heap): https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
7. 블로그(AVL Tree): https://walbatrossw.github.io/data-structure/2018/10/26/ds-avl-tree.html
8. 블로그(Red-Black Tree): https://suhwanc.tistory.com/197?category=730826
(참고문헌 7, 8은 많이 쓰지 않는 개념이지만 존재정도는 알면 좋다. )
'IT > 알고리즘' 카테고리의 다른 글
| [알고리즘(8)] Python으로 알아보는 해쉬테이블 (1) | 2024.12.21 |
|---|---|
| [알고리즘(7)] Python으로 알아보는 그래프(Graph) (3) | 2024.12.07 |
| [알고리즘(5)] Python으로 알아보는 큐(Queue) (2) | 2024.03.16 |
| [알고리즘(4)] Python으로 알아보는 스택(Stack) (0) | 2024.03.15 |
| [알고리즘(3)] Python으로 알아보는 연결리스트(Linked-List) (0) | 2024.03.14 |



